|
|
 |
Mottó: „A tudás olyan, mint egy szent tehén,
és az én problémám az lesz, hogy miképp lehet ezt a tehenet úgy megfejni,
hogy közben távol maradjunk a szarvaitól.” 1
(Szent-Györgyi Albert)
Tartalom
Bevezető gondolatok
Akiket megkérdeztem
Első kérdés: Szereti-e a matematikát?
Második kérdés: Szükség van-e a matematikára
az iskolában?
Harmadik kérdés: Szükség van-e a
matematikára az életben?
Negyedik kérdés: Okoz-e félelmet,
idegességet a matematikaóra?
Ötödik kérdés: Ha sok ideje lenne,
szórakozásból foglalkozna matematikával?
Hatodik kérdés: Átlagosan hány percet
készül egy matematikaórára?
Hetedik kérdés: Mennyire elégedett
a matematikaosztályzatával?
Utolsó kérdés: Melyik témakör tetszett
eddigi tanulmányai során a legjobban?
Összefoglalás
Megjegyzések
az oldal tetejére
Bevezető gondolatok
A tanítás egyik legnagyobb kihívása: a motiválás. Itt elsősorban nem önmagunk motiválására gondolok – habár ez sem mellékes –, hanem tanítványaink érdeklődésének az ébrentartására vagy – ami már keményebb dió – újraélesztésére. Jómagam is gyakran hallom matematikaórán diákjaimtól a kérdést: „miért tanuljuk ezt?”, „hol fogom én ezt használni?”.
Diákjaim fenti kérdései részben jogosak. A szakközépiskolai matematika-tantárgy tartalmi szempontból átgondolásra, jelentős átdolgozásra szorul. Mivel szakközépiskolás tanítványaim döntő többsége közvetlenül a középiskola elvégzése után nem tervez továbbtanulni, így a tananyagban előírt matematikai ismeretek elsajátítása fölösleges szellemi erőfeszítésnek tűnik számukra.
Ám a föltett kérdésből sokszor a matematika-tantárgy, sőt az iskola iránti általános ellenszenv is kicseng. A szorgalmas, érdeklődő kisiskolás, aki örömmel számol, hasonlít össze mennyiségeket, ír le szavakkal formákat, gyakran olyan középiskolássá válik, aki nem leli örömét a matematikával való foglalkozásban.
A matematika megszerettetése, illetve a matematika-tantárgy és ezen keresztül a matematika mint tudomány iránti pozitív érzelmi hozzáállás kialakítása diákjainkban nem csak “mézesmadzag” ahhoz, hogy minél több matematikai ismeretet a diák fejébe gyömöszöljünk, hanem a matematika tanításának egyik célja is.
Szendrei János 7 pontban fogalmazta meg a matematikatanítás céljait.2 Ezek egyike a „…matematikához való jobb hozzáállás kialakítása”. Megjegyzem, hogy Szendrei tanár úr írásában a célok felsorolásakor nem is matematikatanításról, hanem matematikai nevelésről beszél, ezáltal is hangsúlyozva azt, hogy a matematika tantárgy keretében nem egyszerű ismeretközlés/elsajátítás folyik, hanem ennél jóval több.
Ambrus András így ír : „Különösen a matematikatanításban áll fenn a veszélye annak, hogy a tanár csak a kognitív célokra fordítja a figyelmét, amelyek könnyen operacionalizálhatók (műveletekké, tevékenységekké alakíthatók) és ellenőrizhetők, […]. A hetvenes évek közepétől kezdve fordult a figyelem az affektív területek felé. Affektív célokon bizonyos tartós hozzáállást, magatartást értünk az oktatási tartalmakkal kapcsolatban, továbbá tanulási hajlamot, motiváltságot.”3
Annak érdekében, hogy saját diákjaim kifejthessék a matematikához való
viszonyulásukat, néhány kérdést tettem föl nekik, amelyekre írásban, név
nélkül válaszoltak.
az oldal tetejére
Akiket megkérdeztem
Egy szabadkai középiskola hét osztályának tanulóit, összesen 120 főt
kérdeztem meg. A megkérdezettek 74,2%-a lány, és 40,8%-a hároméves, a többiek
négyéves képzésben vesznek részt. Az évfolyamonkénti eloszlást az alábbi
táblázat szemlélteti:
|
|
Százalék |
|
|
|
|
|
|
| 3. | 21,7 |
| 4. | 17,5 |
| Összesen | 100,0 |
az oldal tetejére
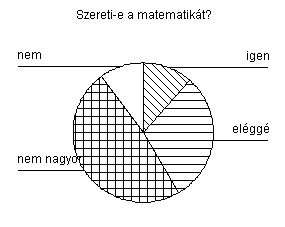
Első kérdés: Szereti-e a matematikát?
„Azok közül, akik bármilyen fokon matematikatanítással foglalkoznak – kisiskolás kortól felfelé –, aligha állíthatná bárki is nyugodt lélekkel, hogy a matematika tanítása körül minden rendben van. Túl sok az olyan gyerek, aki nem szereti a matematikát, és minél idősebb korosztályt tekintünk, annál több.”4 Ez a Dienes Zoltán-idézet a múlt század hetvenes éveiből származik. Vajon ma is érvényes?
Négyféle választ adhattak: „igen”, „eléggé”, „nem nagyon”, „nem”. A felkínált válaszok közül az első kettő pozitív, a második kettő negatív viszonyulást jelent. Semleges válaszadásra („igen is, meg nem is” vagy „közepesen”) nem volt lehetőség, így mindenki valamilyen irányú állásfoglalásra kényszerült.
Habár a kérdés a matematikára mint tudományra vonatkozik, mégis a válaszok valószínűleg a matematika-tantárgyra, sőt még szűkebben a matematikaórára vonatkoztathatók, hiszen a tanulók számára a matematika elsősorban az, amit a matematikaórán megismernek.
Az első kérdésre kapott válaszok eloszlását az alábbi táblázat szemlélteti:
|
|
 |
Az eredmény elég lesújtó. A „nem” és a „nem nagyon” válaszok együttesen 58%-át teszik ki az összes válasznak. A válaszadók képzési idejét figyelembe véve az is kimutatható, hogy a hároméves képzésben résztvevők közül 20,4% adott kategorikus „nem” választ, míg a négyéves képzésben résztvevők közül csak 2,8% volt ez az arány.
A további vizsgálódásokhoz egyesítettem az „igen”–„eléggé” válaszokat, és a „nem nagyon”–„nem” válaszokat. Az előbbit igennek, az utóbbit egyszerűen nemnek vettem.5
Az elemzésekből kitűnt, hogy a négyéves képzésben résztvevőknek nagyjából fele-fele válaszolt igennel, illetve nemmel, míg a hároméves képzésben résztvevők közül ez az arány 30:70 a nemmel válaszolók javára.
Sokan a matematikát „fiús”, a fiúk által kedvelt tantárgynak gondolják.
Ezt a kérdésre adott válaszok nem erősítik meg, sőt enyhén a lányok felé
billen a mérleg. Az általam tanított fiúk 64,5%-a nyilatkozta azt, hogy
nem szereti a matematikát (a fentebben jelzett összevont válaszok szerint),
míg a lányoknál ez a százalékarány valamivel kevesebb, 56,2%.
az oldal tetejére
Második kérdés: Szükség van-e a matematikára az
iskolában?
Az egyetemeken egyre elterjedtebb az a lehetőség, hogy a hallgatók saját
maguk tervezik meg szakmai profiljukat azáltal, hogy – bizonyos korlátozásokkal
– megválaszthatják milyen kurzusokon kívánnak részt venni, mely tantárgyakat
kívánják tanulni. Vajon a felmérésbe bevont szakközépiskolások mennyire
tartják szükségesnek szakmai fejlődésükhöz a matematikát, a matematika
órán tanultakat.
|
|
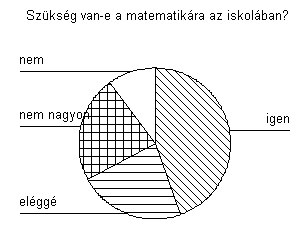 |
Ez előző kérdésre adott válaszok ismeretében kellemes meglepetés a fenti eredmény. Miközben a megkérdezettek 58,3%-a „nem” vagy „nem nagyon” szereti a matematikát (lásd Első kérdés), 67,2%-a (kétharmada!!!) szükségesnek vagy eléggé szükségesnek tartja a matematika jelenlétét az iskolában.
Miután a 4 választ összevontam két válasszá az előző részben ismertetett módon, tovább vizsgálódtam. A 3 éves képzésben résztvevő diákok 44,9%-a adott igen választ, a 4 éves képzésben résztvevők körében ez az arány 82,9% volt.
Még egy érdekességre fölfigyeltem: azok közül, akik nem vagy nem nagyon szeretik a matematikát 55,1% tartja szükségesnek a matematika jelenlétét az iskolában.
Ezek szerint nem olyan rossz a helyzet. Ha választható tantárggyá válna
a matematika, valószínűleg továbbra is sokan tanulnák.
az oldal tetejére
Harmadik kérdés: Szükség van-e a matematikára
az életben?
A második kérdés ismeretében már nagyon bizakodó voltam a pozitív megítélés
szempontjából. Ugyanakkor azzal is tisztában vagyok, hogy az absztrakcióktól
hemzsegő matematika és a hétköznapi élet közötti kapcsolat megláttatása
(tanárnak) és meglátása (diáknak) nem mindig könnyű feladat.
|
|
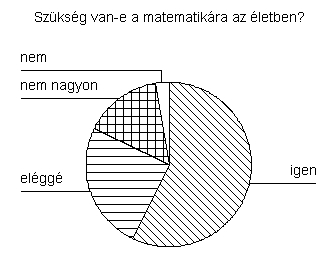 |
A matematika hétköznapi életben betöltött szerepét felismerők döntő többségben vannak. A válaszadók 82,3%-a válaszolt „igen”-nel vagy „eléggé”-vel.
Miután a 4 választ összevontam két válasszá az előző részekben ismertetett módon, tovább vizsgálódtam. A 3 éves képzésben résztvevő diákok 67,3%-a (az előző részben ez 44,9% volt) adott igen választ, a 4 éves képzésben résztvevők körében ez az arány 92,9% (az előbb 82,9%) volt.
Érdekes megfigyelni, hogy míg a lányok a korábbi kérdésekre adott válaszaikat illetően egy árnyalatnyival pozitívabban nyilatkoztak a matematikáról, ez a viszony ennél a kérdésnél megfordult a fiúk javára: A fiúk 87,1%-a szerint van szükség matematikára az életben, a lányoknál ez az arány 80,7%. Ezt a különbséget nem tartom jelentősnek, de a megforduló tendencia azt sugallja, hogy a lányok hajlamosabbak a matematikát egy iskolai gyakorlópályának tekinteni, míg a fiúk jobban észreveszik a mindennapi élettel való összefüggéseit.
Még egy érdekes átfedés: a matematikát szerető tanulóknak 96%-a hasznosnak
tartja e tudományt az életben. Ugyanakkor az életben hasznosnak tartók
közül csak közel fele, 49%-a szereti a matematikát.
az oldal tetejére
Negyedik kérdés: Okoz-e félelmet, idegességet
a matematikaóra?
Az egyik internetes keresőprogram a „matematika” és a „félelem” kulcsszavak
alapján 32400 találatot jelzett. Ennyi szövegben szerepel e két szó ugyanabban
a szövegkörnyezetben. Csak összehasonlításként megjegyzem, hogy a „matematika”
és az „öröm” szavak együttes előfordulása ugyanezen keresőprogram szerint
44700. A mérleg nyelve tehát az „öröm” felé billen – legalábbis a szóelőfordulások
alapján. Az általam megkérdezettek a matematika és a félelem kapcsolatáról
a következő módon vélekedtek:
|
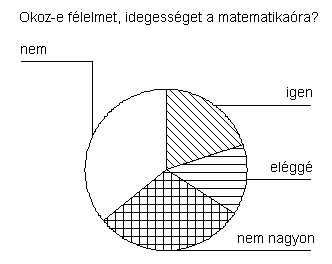 |
Diákjaimnak körülbelül egyharmada válaszolt „igen”-nel vagy „eléggé”-vel. Egyharmaduk számára a matematikaórák mindenféle lelki görcsök, szorongás nélkül múlnak el. A továbbiakban a 4 választ két válaszban sűrítettem a korábban ismertetett módon.
Az évfolyamonkénti eloszlást vizsgálva érdekes jelenségre figyeltem
föl:
|
Az „igen” vagy” eléggé” válaszok évfolyamonkénti eloszlása százalékban kifejezve az adott évfolyam egészéhez viszonyítva
|
Nem tudom, mennyire tudható be a véletlennek, hogy a második évfolyam válaszait leszámítva enyhe emelkedés tapasztalható. Ha nem véletlen, akkor ennek a tendenciának a háttere további vizsgálatot igényel. Azt is érdemes lenne megvizsgálni, hogy ez a növekvő arány csak a matematika tantárgyat érinti, vagy a korcsoportra jellemző tantárgyfüggetlen, általános jelenséggel állunk szemben.
Komoly eltérés mutatkozik a képzési idő szerinti bontásban: a 3 éves képzésben résztvevők közül 58,5% állítja, hogy fél, idegeskedik matematikaórán, míg a 4 éves képzésben résztvevők között ez az arány „csak” 23,9%. Ennek oka véleményem szerint egyrészt abban keresendő, hogy a 3 éves képzésben résztvevők sokkal értelmetlenebbnek látják a velük szemben támasztott követelményeket, mint más iskolatársaik. Másrészt azt feltételezhetjük – habár ebben az irányban nem kutattam –, hogy az ezekbe az osztályokba járók mentálisan labilisabbak, illetve általános problémakezelési modelljeik szegényesebbek, fejletlenebbek.
Számomra teljesen meglepő, hogy fiú tanítványaim 48,4%-a válaszolt „igen”-nel
vagy „eléggé”-vel, míg a lányoknak csak 29,2%-a. Érdemes megjegyezni, hogy
a matematikát szeretők közül csak 12% mondta magáról, hogy fél vagy idegesedik
matematikaórán. A matematikát nem szeretők közül pedig pontosan fele idegeskedik,
fél matematikaórán. Ezek szerint a matematika szeretete a diákoknál maga
után vonja azt, hogy jó közérzettel vesznek részt az órán, a matematika
„nem szeretete” viszont ebből a szempontból nem valószínűsít semmit.
az oldal tetejére
Ötödik kérdés: Ha sok ideje lenne, szórakozásból
is foglalkozna matematikával?
Célunk olyan motivációs környezetet építeni diákjaink köré, amelyben a matematikával való foglalkozás iránti késztetés belsővé válik, és fennmarad akkor is, amikor az általunk létrehozott külső környezet már megszűnik.
Mivel az óráimon láttam, hogy milyen nehéz otthoni munkára ösztökélni
tanulóimat, nem vártam sok jót a válaszoktól. Előzetes várakozásaim beigazolódtak.
|
Ha sok ideje lenne, foglalkozna-e matematikával?
|
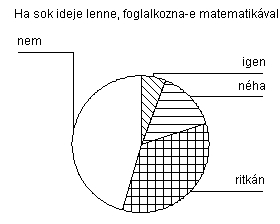 |
A matematikával való foglalkozás nem tartozik a legvonzóbb tevékenységek közé, habár az életben való jelenlétét döntő többségben elismerik (lásd Harmadik kérdés).
A 3 és 4 éves képzésben résztvevők között itt is óriási szakadék van:
előbbiek 67,3%-a, utóbbiak 31%-a válaszolt „nem”-mel. Hasonló arányok figyelhetők
meg a matematikát nem szeretők és szeretők között is.
az oldal tetejére
Hatodik kérdés: Átlagosan hány percet készül egy
matematikaórára?
Itt sem számítottam fölemelő eredményre. Erről gyakran kezdeményezek
beszélgetést tanulóimmal, így tisztában vagyok a helyzettel.
|
A válaszok átlaga 13,78 perc.
A hároméves képzésben résztvevők 19,1%-a, a négyéves képzésben résztvevők 7,4%-a otthon egyáltalán nem készül órára.
Nemrég egyik tanítványom beismerte, hogy egyáltalán nem tanul matematikát
otthon, abból próbál „megélni”, amit órán megtanul. Ezt azzal magyarázta,
hogy általános iskolában úgy volt ötöse, hogy otthon egyáltalán nem kellett
tanulnia. Kollégáimmal való beszélgetésekből is az szűrhető le, hogy középiskolás
diákjainknak nincs semmilyen tanulási technikája, tanulási szokása. Márpedig
e nélkül nem juthatnak előre, mert – André Revuz szavaival – „az erőfeszítés
a matematikától éppúgy elválaszthatatlan, mint a hegymászástól. Nem eltörölni
akarjuk az erőfeszítést, hanem értelemet adni neki, indokolttá tenni.”7
az oldal tetejére
Hetedik kérdés: Mennyire elégedett a matematikaosztályzatával?
Az előbbi kérdéssel ellentétben erről soha nem szoktam diákjaimmal beszélgetni.
Megnyilvánulásaik alapján azonban arra számítottam, hogy túlzott elégedetlenséggel
nem fogok találkozni.
|
Mennyire elégedett a matematika osztályzatával?
|
 |
Feltűnő a viszonylag elégedettek nagy aránya. Feltételezésem szerint a „viszonylag elégedett” válasz mögött az az általános gondolkodás húzódik meg, hogy „a matematikajegyemmel nem vagyok elégedett, de a javulás érdekében nem vállalom a tennivalót, tehát nagyjából jó így, ahogy van”. Pedig lehet, hogy csak a 10 perc tanulást kellene 25 percre növelni? (Lásd Hatodik kérdés)
Megfigyelhető, hogy a megkérdezett fiúk sokkal nagyobb arányban (32,3%) elégedettek az osztályzatukkal, mint a lányok (13,5%).
Ennek a kérdésnek az áttekintésében segít a megkérdezettek osztályzatainak
megismerése. Az alábbi táblázat az általam tanított osztályok félévi összesített
matematikaeredményét tartalmazza.
| osztályzatok: | 5 | 4 | 3 | 2 | 1 | átlag: |
| gyakoriság: | 10 | 26 | 39 | 54 | 9 | 2,81 |
| százalék: | 7,24% | 18,84% | 28,26% | 39,13% | 6,67% | 100% |
Az, hogy ki milyen osztályzattal elégedett, magánügy. Nekem viszont komoly fejtörést okoz, hogy sokszor jó képességű, közepesen vagy az alatt teljesítő diákjaimat hogyan vegyem rá arra, hogy több energiát mozgósítsanak a matematika tanulására.
Sokszor adok föl olyan föladatokat, amelyek nem kötődnek szorosan a tananyaghoz, de megoldásukért valamiféle jutalom jár, amely később ötösre váltható. Többször megtörtént már, hogy egy ilyen feladat hatalmas vitát váltott ki az osztályban, érdekelte őket. Ám odáig nagyon ritkán jutnak el, hogy a következő órára gondolatmenetüket átgondolva leírják, legtöbbször el is felejtik a következő órára. A jó ötletet – és a jó adottságokat – így elmulasztják jegyre átváltani.
A félévkor adott osztályzataim átlaga 2,81. Ez a többi tantárgyhoz viszonyítva
alacsonynak mondható. Szendrei Juliannának erről ez
a véleménye8: „A matematikajegyekből az osztályátlagok
alacsonyabbak, mint más tárgyak átlagai…Érdemes lenne ezt a ’hagyományt’
felülbírálni…Nem hiszem, hogy fontosnak tűnik egy tantárgy, amit olyan
rossz hatásfokkal lehet csak megtanítani.”
az oldal tetejére
Utolsó kérdés: Melyik témakör tetszett eddigi
tanulmányai során a legjobban?
A válaszadók több mint harmada (37,5%) geometriával kapcsolatos témát jelölt meg. Ez számomra azt bizonyítja, hogy a matematikatanítás igen fontos alapelve a szemléletesség. Gondoljunk csak a görög matematikára, ahol a különböző számolásokat is geometriai objektumokkal végezték. Megjegyzem, hogy más, hagyományosan szemléletesen tanított témák (függvények, trigonometria, halmazok,…) is viszonylag gyakran előfordultak a válaszok között.
A második legnépszerűbb témaként (27,5%) a négy alapművelet valamelyikét nevezték meg. Ennek az is lehet az üzenete, hogy már régen nem találkoztak matematikaórán olyan témával, amely igazán érdekelte volna őket. Az is nyilvánvaló, hogy legszívesebben olyan témakörre emlékeznek vissza, amelynek tanulásával volt sikerélményük és ezt kisiskolás koruk óta nem nagyon élték meg.
A harmadik helyet a népszerűségi listán (14,2%) két témacsoport osztja: az algebrai kifejezésekkel illetve különböző egyenletek és egyenletrendszerek megoldásával kapcsolatosak. Mivel e két témakörben való sikeresség a tanulótól szabályok illetve algoritmusok alkalmazását követeli meg, így ez elsősorban azoknak lehet a kedvence, akik kreativitásukat a matematikában nehezen bontakoztatják ki, viszont megfelelő szorgalmuk révén sikerélményhez tudnak jutni. „A tanuló számára akkor kedves az óra, ha azon jól szerepelt; a jegy nem is olyan fontos, mint a szereplés sikere. […] Szakkörön megfigyelhető, hogy amelyik tanuló nem jut szerephez, az elmarad.”9
az oldal tetejére
ÖSSZEFOGLALÁS
A fenti fölmérés számomra a következő tanulságokkal szolgál:
· A matematikát nem nagyon kedvelik a diákok, de
az iskolában való jelenlétét igazoltnak tarják, és az életben pedig még
szükségesebbnek ítélik meg.
· A lányok egy kicsivel jobban szeretik a matematikát,
de a matematikát elsősorban iskolai tantárgynak tekintik. A fiúk az életben
való szükségességét jobban belátják, de a matematikaóra több félelmet,
idegességet kelt bennük, mint a lányokban. A fiúk általában elégedettebbek
az osztályzataikkal.
· A hároméves képzésben résztvevők kevésbé szeretik
a matematikát, nem látják szükségességét a tanulásának az iskolában, frusztrálja
őket a matematikaóra. Szükségesnek tartják a matematikát az életben. A
3 éves képzésben résztvevők között nagyobb arányban vannak olyanok, akik
egyáltalán nem készülnek órára.
· Aki a matematikát szereti, az hasznosnak is tartja
(fordítva nem feltétlenül igaz).
· Aki a matematikát szereti, az szívesen, félelem
nélkül vesz részt az órán (fordítva nem feltétlenül igaz).
· A matematikát kevesen kedvelik meg annyira, hogy
később is foglalkozzanak vele.
· Diákjaink munkaszokásának, tanulási technikáinak
kialakítására, fejlesztésére fokozottan oda kell figyelnünk.
· A matematikatanításban jobban törekednünk kell
a szemléltetésre, és fontos a tanulót a lehetőségekhez mérten minél több
sikerélményhez juttatni.
Ezek a következtetések nem általános érvényűek, hiszen csak egy adott iskola egy adott matematikatanára által tanított diákjainak válaszai alapján születtek meg. Ennek ellenére mégis hasznosak lehetnek, hiszen közös gondolkodásra késztethetnek bennünket.
Tanulmányomat egy Szent-Gyögyi-idézettel kezdtem, egy másik gondolatával
fejezem be: „Ilyenképpen az, amit az iskolának el
kell végeznie, elsősorban az, hogy megtaníttassa velünk, hogyan kell tanulni,
hogy felkeltse a tudás iránti étvágyunkat, hogy megtanítson bennünket a
jól végzett munka örömére és az alkotás izgalmára, hogy megtanítson arra,
hogy szeressük, amit csinálunk, és hogy segítsen megtalálni azt, amit szeretünk
csinálni.”10
-------------------------------------------------------------
Megjegyzések:
1 Szent-Györgyi Albert:
Az élet jellege, Magvető Kiadó, Budapest, 1975, 37. old.
2 Szendrei János.
In Vörös György [szerk.]: Szemelvénygyűjtemény a matematika tanításához,
Tankönyvkiadó, Budapest, 1987, 14. old.
3 Ambrus András:
Bevezetés a matematikai didaktikába, ELTE Eötvös Kiadó, 1995, 23. old.
4 Dienes Zoltán:
Építsük fel a matematikát, Gondolat, Budapest, 1973, 21. old.
5 Az idézőjelek
között szerepeltetett „igen” és az idézőjelek nélkül írott igen között
különbség van. Az előbbi a kérdőíven választható válaszra vonatkozik, az
utóbbi pedig a válaszok földolgozása során általam bevezetett válaszcsoportra
(például az „igen” és „eléggé” válaszok egyesítésére). Ez a megjegyzés
a táblázatokra és grafikonokra nem érvényes.
6 Ne tévessze meg
az olvasót, hogy az előző táblázatokkal ellentétben e táblázat sorai nem
diszjunkt halmazokat neveznek meg. Például az, aki legfeljebb 10 percet
tanul matematikát, az beleszámít azok közé is, akik legfeljebb 15 percet
tanulnak, tehát emiatt a százalék oszlopában szereplő számok halmozódó
százalékértékek – természetesen az utolsó sor kivételével.
7 André Revuz: Modern
matematika – élő matematika, Gondolat, Budapest, 1973, 106. old.
8 Szendrei Julianna:
Gondolod, hogy egyre megy?, Typotex Kiadó, Budapest, 2005, 382–383. old.
9 Cser Andor [szerk.]:
A matematikatanítás módszertanának néhány kérdése, Tankönyvkiadó, Budapest,
1972, 264. old.
10 Szent-Györgyi Albert:
Az élet jellege, Magvető Kiadó, Budapest, 1975, 41. old.